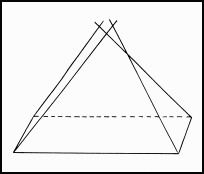
Hypothetical pyramid lacking "control."
(Originally published in The Ostracon, Vol. 12, No. 1, Summer 2001.
The Ostracon is a Journal of the Egyptian Study Society, Denver, CO.
© Copyright: Bonnie M. Sampsell. No part may be reproduced.)
What is it about Egyptian pyramids that fascinates us so? Surely their enormous size and great age command our respect. But most impressive may be their stark simplicity of form and perfect shape. For generations people have wondered how the ancients were able to build such structures with only simple tools.
Skeptics have claimed “with the means at their disposal the ancient Egyptian would have found it impossible to raise a true pyramid from the ground since misalignment of the edges cannot be corrected at a later building stage. A small error of only 2° would lead to a mismatch of 15 metres at the top of one of the Giza pyramids” (Mendelssohn 1974:116). A diagram such as Figure 1 usually accompanies such a statement. But this diagram is nonsense! Mistakes in laying the blocks might lead to a less-than-perfect shape, but it is impossible for the problem shown here to occur. The four faces will certainly meet at a single point in the sky although it may not be the one desired by the ancient architect.
Figure 1

Hypothetical pyramid lacking "control."
Modern architects use the word "control" to describe the methods whereby the design of a building is achieved. Few aspects of pyramid building have attracted more attention or produced less of a consensus than this one. I plan to outline the challenges associated with maintaining architectural control, review a few of the solutions previously offered to this problem -- none of which solves it to my satisfaction -- and finally propose a simple solution that was entirely within the capabilities of the ancient Egyptians.
Kurt Mendelssohn (1974), Martin Isler (1987), and others have insisted that the only way that the Egyptians could have built a true pyramid without distortion was first to build a step pyramid to its full height and then place a marker on the top of this core to mark the final apex and to serve as a guide in placing the casing blocks. These authors find evidence for such an approach in the observation by M. A. Martin who climbed the Meidum Pyramid in 1899 in order to place a survey marker at its apex. He found that there already was a hole for such a marker in the top of the pyramid. But this hole is unlikely to have been one used by ancient Egyptians since the point in which it occurs was not the top of the ancient seven-step pyramid but many feet below that. A pole placed on the current peak would have to be an unmanageable 75 feet high to indicate the apex of the true pyramid that was built over the step pyramids.
Other authors, including Michael Lally (1989) and George Johnson (1994), have also proposed that a step-pyramid core was built first and the final pyramidal casing was sited by measuring from the steps of this core. As Johnson (1994:81) said,
All Old Kingdom pyramids appear to have stepped cores. It should be noted that these steps -- or buttress walls or accretion faces -- do not represent a series of mastabas within the structures, but only the continuation of the traditional benchmark-system of construction that had been developed for the building of mastabas. The benchmarks are the true framework of a pyramid. Once they were established, all problems of measurement, layout and alignment were solved within the structure of a pyramid, not at the outside casing faces. [Emphasis added.]
But we now know that from Dynasty IV onwards true pyramids were not built with internal accretion layers, nor did the largest ones such as the Bent and Red at Dahshur or Khufu’s or Khafre’s at Giza have steps or stages in their cores (Sampsell, 2000). In fact, considerable evidence suggests that these gigantic pyramids were built up one horizontal course at a time with both core and casing blocks of each course set before proceeding to the next course. Meidum is the only step pyramid that has been measured, and it departs from perfect symmetry in many ways (Petrie 1892:6-7). Thus its steps could not have served as reference points to place the casing of the true pyramid built over it.
Alexander Badawy proposed another method for maintaining control that draws on an observation made by Flinders Petrie while excavating the huge, mud brick mastaba No. 17 next to the Meidum Pyramid. Petrie found that an L-shaped vertical wall had been built at each corner of the mastaba’s base (Petrie 1892:12). On the inner sides of the wall, lines were drawn at a 75° angle. These lines were presumably used during the laying of the mud bricks in the outer wall of the mastaba to ensure that the mastaba face conformed to the angle drawn on the brick wall. Such a method, however, could not have been applied in the construction of a megalithic stone pyramid because the distance along the pyramid face to the corner was too great for accurate sightings or to stretch a cord. Dieter Arnold (1991:12) said “How the men laying the bricks [at Mastaba No.17] transferred these markings to the walls is not known. Since the mastaba walls are too long to be checked by the human eye (52.5 x 105.0 meters) and too long for stretching a cord (which would sag in the center) ...” If builders could not sight 300 feet along a mastaba wall, a 760-foot pyramid face is clearly much too long for this method.
Somers Clarke and Reginald Engelbach, avid investigators of ancient Egyptian architecture and technology, struggled with the question of control. Because they assumed that the builders would need to have work-face platforms or embankments up to forty feet wide in front of each face that would obscure the face from view, they opted for a control system involving plumb lines (Clarke and Engelbach 1990:125-6). They believed that the casing blocks were laid with their faces still roughly vertical and that the correct slope of the face was drafted onto the blocks by measuring from the plumb line. Final finishing to the face was performed later from the apex of the pyramid downwards as the work-face embankment was removed. Clarke and Engelbach felt that to avoid cumulative errors that would arise if this procedure were applied course by course, the plumb lines would have to be suspended in pits up to 17 feet deep, so that only about 30 shifts of position would be needed during the entire process of raising the Great Pyramid. Several pits would have been needed along each face, however, to provide a reference line for each course.
Figure 2

Method proposed by Clarke and Engelbach to achieve "control" during pyramid construction.
Looking at Figure 2, we can see some of the problems that this method would encounter: maintaining a deep well in the work-face platform and making accurate measurements across an increasing horizontal distance. In any case, such an approach still requires that the desired angle of inclination be reproducible at each level. Since this is so, a much simpler method suggests itself, as I will explain shortly.
The problem of architectural control is intimately related to the issue of access ramps, and many people have objected to spiral or other face-hugging ramps (as presumed by Clarke and Engelbach, for example) on the grounds that pyramid faces and edges had to be kept clear during construction so that sightings could be taken along them. Endless debate has raged about the shape of access ramps and whether any were used at all. A new proposal about the shape of access ramps at Giza and a different idea about control of pyramid shape simultaneously resolve many of the old problems.
Mark Lehner has presented convincing arguments that a straight access ramp approached the Great Pyramid from the quarries and harbor to the south and ran up to a height of about 100 feet at the southwest corner; from there it continued as a spiral ramp around the west, north, and east faces (Lehner 1985:109-143; Lehner 1997:215–217). He believes this access ramp rose in height as the pyramid itself was built; in addition, from the beginning a work-face embankment completely encircled the pyramid rising course by course to maintain a surface level with the course under construction. After many years of studying various proposals concerning ramps, I feel that Lehner offers the best solution: the straight section of ramp was short enough not to overshoot the quarries, the spiral ramp used less material than any other configuration, the access ramp blended into the work-face embankments in an economical fashion, the spiral ramp was stable since it rested on the ground and the completed pyramid faces, no retaining walls were needed, and finally the ramp constituents (limestone rubble from quarrying and desert clay) were abundant and could be easily recycled when construction was complete.
But, if as Lehner suggested all surfaces of the rising pyramid were covered with ramps, how did the builders control its shape? I had pondered this question for several years when a new idea occurred to me that would solve all the problems. Then when Lehner’s book, Complete Pyramids, appeared, I discovered that he offered almost the same solution, a fact that gave me great encouragement. My proposal does differ from his in one crucial respect, however. Before explaining these two proposals, I will consider more carefully the potential problems that the pyramid builders faced, since such a study also suggests solutions.
Figure 3 illustrates several potential problems or variations from the ideal pyramid shape one at a time. Each problem has been exaggerated for emphasis. For each example, the plan of a small pyramid is shown at the top with the lines indicating the front edges of successive courses. The cross-section of each pyramid is shown below it. Part A. shows an ideal pyramid: it is square at each level, the corners form right angles (90°), the two diagonals of each course are equal, each face has the uniform slope of 52°, and the apex lies directly over the intersection of the two diagonals.
Figure 3
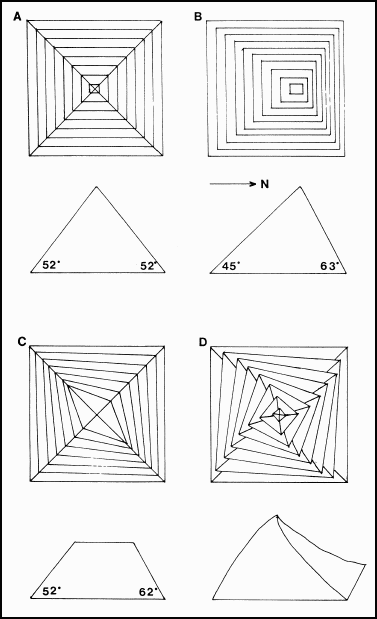
True pyramid and those deviating from perfect shape.
In Figure 3, Part B, the corners form right angles and the two diagonals are equal for each course, but the apex drifts off center. Looking at the cross-section below we see that while the east and west faces retain the desired slope of 52o, the north face rises at an angle of 62° while the south has a slope of only 44°.
In Figure 3, Part C, the square of the base becomes more distorted at each course. The corners are either greater than or less than 90°; the diagonals are not equal. By the sixth course, if the courses remain level, the face angle near the northeast corner is nearly 62°.
In Figure 3, Part D, the corners are right angles, the two diagonals are equal, and the intersection of the diagonals remains centered, but each course is twisted or rotated (the twist is greatly exaggerated in the figure) compared to the one beneath it. We can see that this problem arises unless each corner casing block is placed with its ridge in line with that on the block below it.
Any combination of these problems might occur causing the pyramid, as built, to deviate from the ideal form. In actual practice, either errors by the masons in carving the slopes into the blocks or sloppiness by builders in placing them could be the cause of the changes in pyramid shape. In fact, the Giza builders seem to have been quite successful in building to the ideal shape. Piazzi Smyth (1867:165) used a sextant to sight up each face of the Great Pyramid. In spite of the roughness of the faces due to the missing casing, he estimated the slopes as follows: 51° 39' (north), 51° 46' (east), 51° 54' (south), and 51° 42' (west). So we see that the slopes were maintained nearly constant on all four sides. In the case of the Khafre Pyramid, Petrie detected an angular twist of only 1' 40" in a counterclockwise direction (Petrie 1883:97). It should also be mentioned that if small errors of shaping and setting did occur, it is more likely that they would be random and compensating rather than cumulative as in Figure 3. The task of the overseers was to prevent systematic and growing deviations from the plan.
As noted above, and by many authors, measuring the diagonals and keeping them equal would have provided a useful element of control during construction. Unfortunately this was not possible at the base of any of the three large Giza pyramids since bedrock knolls had been left in the middle of their sites when the ground was leveled prior to construction. In the Great Pyramid, the height of this knoll has been estimated to be around 23 feet, or less than 5% of the entire height (Maragioglio and Rinaldi 1965:12). Thus during most of the construction at the upper levels such diagonal measurements could have provided an invaluable check to prevent the kind of distortion illustrated in Part C.
The inspiration for my new idea for control came from the realization -- as I studied this diagram -- that all of these problems could be prevented by the accurate shaping and setting of the casing blocks one course at a time. In this way the slope could be maintained constant, the corners squared, and the sides equal. Lehner calls his similar proposal “designing [the] slope stone by stone” (Lehner 1997:220-1). According to his description and diagrams [see page 220 of Complete Pyramids] the casing blocks, with their horizontal bedding (lower) surface already prepared, were brought to their final location where they were trimmed to match the adjoining casing stone already laid. They were levered into position using a film of gypsum mortar as a lubricant; then they were marked with their correct slope and dressed there in situ.
There is excellent evidence that the vertical front faces of the casing stones were cut to the correct slope at the time they were set into position. For example the granite casing blocks, still in place at the base of Menkaure's Pyramid have vertical edges inclined at about 53°, although the faces retain excess material. And as Dieter Arnold said (1991:169): “Only the surfaces around the entrance and behind the offering chapel had been dressed and ground when the work was abandoned. All the other blocks still have their extra stock, some even with additional handling bosses. In order to facilitate the exact placement, the edges had been chamfered back to the intended sloping surface.” [Emphasis added]
The same thing can be observed on the casing blocks of the steps at the Meidum Pyramid many of which were NOT smoothed subsequent to placement because they were covered by the accretion layer in front of them. These became visible only when a portion of the pyramid collapsed. Note that Arnold implies that the edges of the casing stones were cut to the desired slope before the blocks were placed, not afterwards as Lehner shows in his diagram. Note also the difficulty that Lehner’s builders will face as they attempt to lay the second course of casing with a work-face ramp covering the first course and the reference line. Lehner never discusses the problems associated with retaining access to this reference line throughout the building process.
Perhaps, I should have mentioned before that my use of degrees to measure slopes is not the way that ancient Egyptians would have done it. They represented slopes using a concept called the seked that was defined as the horizontal displacement (sometimes called “run”) for a rise of one cubit. (I was intrigued to learn that carpenters still use the method of rise and run when building roofs or staircases.) Since each cubit was divided into seven palms each of which contained four fingers, a change in the seked of a slope by one finger involved an angle of little over one degree. Thus fairly fine gradations of slope could be specified. The slope of the Great Pyramid, measured at 51° 52’, could be represented by a seked of 5 palms and 2 fingers, while Khafre’s Pyramid with a slope of 53° 10’ has a seked of 5 palms and 1 finger. See Figure 4.
Figure 4
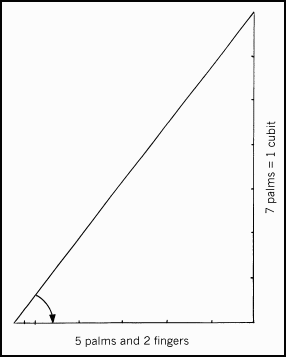
Ancient Egyptian method of determining slopes.
This angle has a seked of 5 palms and 2 fingers.
Once the king chose a slope for his pyramid, this slope could be drawn, copied, reproduced, and checked as many times as necessary using only a cubit rod. The royal architect and overseers of stone masons could also have produced a large number of identical patterns, formed of two pieces of wood joined at the proper angle, for the dozens of stonecutters to use in drafting the correct slopes onto the casing blocks. In addition, by carefully chiseling a trial block with the proper slopes on two adjacent faces, the correct slope of the corner angle could be determined.
My idea for control differs significantly from Lehner’s because I propose that the casing blocks were cut to their final shape (with the exception of excess material left on the face and even here there is some room for doubt) on the ground in a stone yard under the close supervision of a master mason and not on the rising pyramid. Thus I propose that the upper and lower faces were made perfectly parallel, fixing also the final height of the block. The sides of adjacent blocks were cut to perfect matches and the blocks marked for their respective positions. Then the masons cut the vertical edges of the front face to the precise slope of the pyramid's face using the patterns previously described. All four edges of the front of the stone thus corresponded to its final shape. Corner casing blocks were cut with special care so the two adjacent faces met in the correct slope of the ridgeline and also formed a perfect right angle.
The block setters had the critical task of setting each prepared casing stone correctly on the course beneath it by aligning the prepared edges. The corner blocks of a course were set first, and adjacent blocks wedged tight against these continuing across the face on each side (Arnold 1988:54-56). At Meidum, tiny blocks often reveal the last stone set in the middle of a row of casing on the inner steps, but this problem was probably avoided in later pyramids.
What this procedure does is create a new “reference line” at each course of blocks: the front edges of the blocks. Since each block has already been shaped to the correct slope (at least at the edges) no further measurements of angles are necessary. Constructing the casing of each course in this manner maintained the essential shape of the entire pyramid. Core blocks only had to be set within the perimeter defined by the casing.

This process can be better visualized by referring to the childhood experience of many of us who had sets of building blocks. Those who had the forerunners of Lego type building blocks could construct walls of excellent verticality with right-angled corners because the rectangular blocks only locked together in such a fashion. Imagine then a set of toy blocks consisting mostly of uniform cubes, some blocks with one face cut at a 45° angle, and a few blocks with two such sloping faces meeting at 35° corner. Even a careful child could build a perfect pyramid with no measuring or sighting whatsoever. (Note: In this article, I have completely ignored the problem of laying out the pyramid initially on a square base with the desired celestial orientation. I dealt only with the issue of achieving the ideal pyramidal shape given a carefully surveyed base.)

REFERENCES:
Arnold, Dieter. 1988. “Manoeuvring casing blocks of pyramids.” In Pyramid Studies and Other Essays Presented to I. E. S. Edwards, edited by John Baines, T.G.H. James, Anthony Leahy, and A. F. Shore. London: Egyptian Exploration Society. Pp 54-56.
Arnold, Dieter. 1991. Building in Egypt. New York: Oxford University Press.
Badawy, Alexander. 1977. “The Periodic System of Building a Pyramid.” Journal of Egyptian Archaeology 63:52-58.
Clarke, Somers and R[eginald] Engelbach. 1990. Ancient Egyptian Construction and Architecture, New York: Dover Publications, Inc. This is a reissue of the book Ancient Egyptian Masonry published in 1930 by Oxford University Press, London. This earlier publication date should be borne in mind in evaluating the contents.
Isler, Martin. 1987. “On Pyramid Building II.” Journal of the American Research Center in Egypt XXIV:95-112.
Johnson, George. 1994. “The Meidum Pyramid. Part 2.” KMT 5(1):72-82.
Lally, Michael T. 1989. “Engineering a Pyramid.” Journal of the American Research Center in Egypt XXVI:207-218.
Lehner, Mark, 1985. “The Development of the Giza Necropolis: The Khufu Project.” Mitteilungen des Deutschen Archäologischen Instituts Abteilung Kairo 41:109-143.
Lehner, Mark. 1997. The Complete Pyramids. New York: Thames and Hudson.
Maragioglio, Vito and Celeste Rinaldi. 1965. L’Architettura delle Piramidi Menfite, Parte IV. Rapallo: Tipografia Canessa.
Mendelssohn, Kurt. 1974. The Riddle of the Pyramids. New York: Praeger Publishers.
Petrie, W. M. Flinders. 1883. The Pyramids and Temples of Gizeh. London: Field & Tuer Ye Leadenhalle Presse.
Petrie, W. M. Flinders. 1892. Medum. London: David Nutt.
Sampsell, Bonnie. 2000. “Pyramid Design and Construction, Part I: The Accretion Theory.” The Ostracon 11(3):2-6.
Smyth, Piazzi. 1867. Life and Work at the Great Pyramid, vol. II. Edinburgh: Edmonston and Douglas.
© Copyright Bonnie M. Sampsell.
Catchpenny Mysteries © copyright 2000 by Larry Orcutt.