Piazzi Smyth, Our Inheritance in the Great Pyramid, plate II

Piazzi Smyth, Our Inheritance in the Great Pyramid, plate II
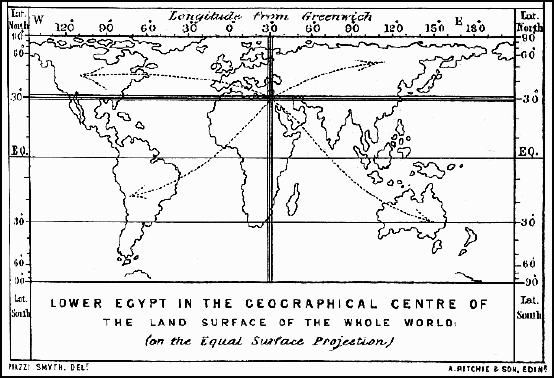
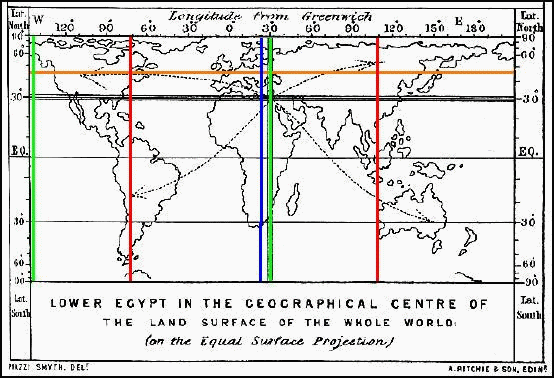
One of the popular oft-repeated claims made about the Great Pyramid was described by Piazzi Smyth in Our Inheritance in the Great Pyramid (1880). He wrote that "proceeding around the globe due north and due south of the Great Pyramid ... there is more earth and less sea in that meridian than in any other meridian all the equator round." (p. 89) Of course, the earth is a globe, not a flat projection. Smyth's meridian (in green below) crosses very little land on the other side of the earth, while a meridian near 70° W (in red below) crosses much more land on its way round the globe. If by "meridian" Smyth means a half-circle, then the claim's accuracy may still be disputed (it is entirely anecdotal and no mathematical proof has been offered). It appears that a meridian a few degrees to the west (in blue below) would cross more land.
Piazzi Smyth, Our Inheritance in the Great Pyramid, plate II
Smyth also asserts that "taking the distribution of land and sea in parallels of latitude, there is more land-surface in the Great Pyramid's general parallel of 30°, than in any other degree ..." (p. 89) Again, this is doubtful. A line of latitude several degrees north (in orange above) traverses more land. Smyth further claims that "on carefully summing up the areas of all the dry land habitable by man all the wide world over, the centre of the whole falls within the Great Pyramid's special territory of Lower Egypt." (p. 89) The earth's landmass is distributed over a sphere, not a plane. Thus, determining "center point" of the landmasses -- and there would of necessity be more than one such center point as the lines wrapped around the globe to the other side -- would be a complex affair based on the area of each continent and every little island in the seas. That these points legitimately exist at all is questionable.
In addition to their inaccuracy, Smyth's claims fail to consider why the geographical center of the planet's landmass might have been so compellingly important to the ancient Egyptians. There is nothing in the corpus of what is known about ancient Egyptian culture or religion that would suggest such an obsession. It is implicit in Smyth's contentions that the Egyptians settled in the Nile Valley because of the area's relation to the globe's landmass rather than for any environmental advantage it had to offer. One can only wonder that if Smyth's "magical point" fell instead in, say, southern Indiana, the Egyptians would have settled and built their pyramids there.
Piazzi Smyth wrote, "I have never accused, and do not propose to tax, those profane Egyptians with having had anything to do with the design of the Great pyramid." (p. 90) He held them in contempt, writing of "Egyptian idolaters," their "peculiar and alas! degrading religion," and their "vile hieratic system." (p. 6) Then by whom was the Great Pyramid designed? While many contemporary writers like to attribute its authorship to extraterrestrials or Atlanteans, it was Smyth's contention that it was designed by God Himself "'to be for a sign and for a witness unto the Lord of Hosts in the land of Egypt.'" (p. 596) He quotes here from Isaiah 20:20; indeed, it is frequently stated that Isaiah 19:19 is a Biblical reference to the Great Pyramid:
In that day there will be an altar to the Lord in the midst of the land of Egypt, and a pillar to the Lord near its border.
That the Great Pyramid is not at Egypt's border is generally explained away in various manners, but the context of the verse is wholly ignored. For one thing, Isaiah wrote no earlier than the 8th century BC, at which time the Great Pyramid was already ancient; yet he writes of the altar in the future tense. The prophesies contained in verses 16 through 25 all occur "in that day," that is, in the in the coming day of the Lord (cf. 11:10-12). Taken in the context of previous verses and those that follow, it is clear that the events described have not yet taken place, including the erection of the "altar to the Lord" described in 19:19. This could not, then, refer to the Great Pyramid. Despite this rather obvious conclusion, a myriad of books have been written about the Great Pyramid as a medium for Biblical prophesy.
In his book Armageddon: Appointment With Destiny (1988), author Grant Jeffrey writes (Page 233):
The word ark comes from the Hebrew word aron, which means a chest, box, or coffin. Its dimensions are described by the Bible as 2.5 cubits by 1.5 cubits by 1.5 cubits (45 inches by 27 inches by 27 inches). Curiously, this is the exact volume of the stone chest or porphyry coffer in the King's Chamber in the Great Pyramid in Egypt. This coffer was the only object in the King's Chamber, as the Ark was the single sacred object within the Holy of Holies, in the Temple. Also, the laver, or basin, that the priests used to wash their feet had the identical cubit dimensions.In addition, the cubit dimension of the inner chamber of the Temple, the Holy of Holies, are precisely identical in size to the King's Chamber in the Pyramid and the same volume as the molten sea of water on the Temple Mount as prepared by King Solomon. Since the Pyramid was built and sealed long before the days of Moses, when he built the Ark and the Holy of Holies, and had remained sealed for over twenty-five centuries until the ninth century after Christ, there is no natural explanation for the phenomenon of both structures having identical volume measurements. The coffer in the pyramid contains exact measurements representing tremendous scientific knowledge as does the entire Great Pyramid. A small example of this data is that the height of the pyramid is precisely one billionth the distance of the earth from the sun.
Is this information correct? Most readers of Jeffrey's book lack either the resources or the ambition to check out his data. Many people take such claims on faith, but let's check (the linear dimensions are given in inches and the volume in cubic inches):
| Description | Width | Height | Length | Volume |
|---|---|---|---|---|
| The Ark | 27.0 | 27.0 | 45.0 | 32,805 |
| Coffer (inner) | 26.8 | 34.4 | 78.1 | 72,002 |
| Coffer (outer) | 38.5 | 41.3 | 89.6 | 142,468 |
| Laver* | 56,115 |
*Described in I Kings 7:38 (one bath equals 6.073 gallons).
Obviously, the dimensions of the Ark and the coffer differ markedly.
The Coffer in the King's Chamber.

© Photo copyright Larry Orcutt
The Holy of Holies in the Temple measured 20 cubits by 20 cubits by 20 cubits (I Kings 6:20). Moses did not build his Holy of Holies in a Temple as Jeffrey implies, but in his Tabernacle (Moses' Holy of Holies measured 10 cubits by 10 cubits by 10 cubits). The molten sea was round and is described in I Kings 7:23-26.
| Description | Width | Height | Length | Volume |
|---|---|---|---|---|
| Holy of Holies (Temple) | 360 | 360 | 360 | 46,656,000 |
| Holy of Holies (Tabernacle) | 180 | 180 | 180 | 5,832,000 |
| King's Chamber | 206 | 229 | 412 | 19,435,688 |
| Molten sea | 180 | 90 | 2,805,726 |
The dimensions for the Holy of Holies and the King's Chamber are far from being "precisely identical" as Jeffrey asserts.
What about Jeffery's claim that "height of the pyramid is precisely one billionth the distance of the earth from the sun?" The height of the Great Pyramid is 485 feet:
Okay, so what's a million miles or so? Astronomically, the numbers may be close, but is this similarity meaningful, or even interesting? Following is an excerpt from Umberto Eco's excellent book Foucault's Pendulum, chapter 48 (the discussion concerns Piazzi Smyth's classic pyramid tome, Our Inheritance in the Great Pyramid, published in 1880 and still in print):
"I imagine that your author [Smith] holds that the height of the pyramid of Cheops is equal to the square root of the sum of the areas of all its sides. The measurements must be made in feet, the foot being closer to the Egyptian and Hebrew cubit, and not in meters, for the meter is an abstract length invented in modern times. The Egyptian cubit comes to 1.728 feet. If we do not know the precise height, we can use the pyramidion, which was the small pyramid set atop the Great Pyramid, to form its tip. It was of gold or some other metal that shone in the sun. Take the height of the pyramidion, multiply it by the height of the whole pyramid, multiply the total by ten to the fifth, and we obtain the circumference of the earth. What's more, if you multiply the perimeter of the base by twenty-four to the third divided by two, you get the earth's radius. Further, the area of the base of the pyramid multiplied by ninety-six times ten to the eighth gives us one hundred ninety-six million eight hundred and ten thousand square miles, which is the surface area of the earth. Am I right?"Belbo liked to convey amazement with an expression he had learned in the cinematheque, from the original-language version of Yankee Doodle Dandy, starring James Cagney: "I'm flabbergasted!" This is what he said now. Aglie also knew colloquial English, apparently, because he couldn't hide the satisfaction at this tribute to his vanity. "My friends," he said, "when a gentleman, whose name is unknown to me, pens a compilation on the mystery of the pyramids, he can only say what by now even children know. I would have been surprised if he had said anything new."
"So the writer is simply repeating established truths?"
"Truths?" Aglie laughed, and again opened for us the box of his deformed and delicious cigars. "Quid est veritas, as a friend of mine said many years ago. Most of it is nonsense. To begin with, if you divide the base of the pyramid by exactly twice the height, and do not round off, you don't get pi, you get 3.1417254. A small difference, but essential. Further, a disciple of Piazzi Smyth, Flinders Petrie, who also measured Stonehenge, reports that one day he caught the master chipping at a granite wall of the royal antechamber, to make his sums work out ... Gossip, perhaps, but Piazzi Smyth was not a man to inspire trust; you had only to see the way he tied his cravat. Still, amid all the nonsense there are some unimpeachable truths. Gentlemen, would you follow me to the window?"
He threw open the shutters dramatically and pointed. At the corner of the narrow street and the broad avenue, stood a little wooden kiosk, where, presumably, lottery tickets were sold.
"Gentlemen," he said, "I invite you to go and measure that kiosk. You will see that the length of the counter is one hundred and forty-nine centimeters -- in other words, one hundred-billionth of the distance between the earth and the sun. The height at the rear, one hundred and seventy-six centimeters, divided by the width of the window, fifty-six centimeters, is 3.14. The height at the front is nineteen decimeters, equal, in other words, to the number of years of the Greek lunar cycle. The sum of the heights of the two front corners and the two rear corners is one hundred and ninety times two plus one hundred seventy-six times two, which equals seven hundred and thirty-two, the date of the victory at Poitiers. The thickness of the counter is 3.10 centimeters, and the width of the cornice of the window is 8.8 centimeters. Replacing the numbers before the decimals by the corresponding letters of the alphabet, we obtain C for ten and H for eight, or C10H8, which is the formula for naphthalene."
"Fantastic," I said. "You did all these measurements?"
"No," Aglie said. "They were done on another kiosk, by a certain Jean-Pierre Adam. But I would assume that all lottery kiosks have more or less the same dimensions. With numbers you can do anything you like. Suppose I have the sacred number 9 and I want to get the number 1314, date of the execution of Jacques de Molay -- a date dear to anyone who, like me, professes devotion to the Templar tradition of knighthood. What do I do? Multiply nine by one hundred and forty six, the fateful day of the destruction of Carthage. How did I arrive at this? I divided thirteen hundred and fourteen by two, by three, et cetera, until I found a satisfying date. I could also have divided thirteen hundred and fourteen by 6.28, the double of 3.14, and I would have got two hundred and nine. That is the year in which Attalus I, king of Pergamon, joined the anti-Macedonian League. You see?"
Catchpenny Mysteries © copyright 2000 by Larry Orcutt.